#数楽 以下のリンク先がきっかけになって、「LU分解ブーム」が来ているらしい。ちなみに、LU分解X=LUを使ってXに関する簡単な線形方程式を書き直した結果はソリトン方程式の理論において佐藤・ウィルソン方程式と呼ばれています。https://twitter.com/sho_yokoi/status/839066592428220417 …

#数楽 例えば、dX/dt=XAをLU分解X=LUを使って書き直すと、(dL/dt)U+L(dU/dt)=LUA、∴L^{-1}dL/dt+(dU/dt)U^{-1}=UAU^{-1}なので、UAU^{-1}の対角成分を除く下三角部分をB=(UAU^{-1})_-と書くと〜続く

#数楽 L^{-1}dL/dt=B、(dU/dt)U^{-1}=UAU^{-1}-BすなわちdL/dt=LBdU/dt=UA-BUとなります。これが所謂Sato-Wilson方程式。KdVの類もこの形で書ける。Aはtによらない定数だが、Bはそうでないことに注意。続く

#数楽 続き。Uの方の非自明な対角成分が佐藤のτ函数で、Xの左上ブロックの主小行列式になります。だから、τ函数は行列式で書ける。このように、ソリトン方程式の佐藤理論は大学一年生レベルの線形代数を知っていれば理解できます！実際には無限次元化の部分がちょっと面倒なのですが。

#数楽 極めてシンプルなソリトン方程式の基本パターンについては→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/#soliton …極めてシンプルな話(大学一年生レベルに近い話)なので、詳細に入る前の段階で、ごちゃごちゃと複雑に見えていたら、「誤解している」ということになると思う。

#数楽 佐藤幹雄講義録は http://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/215756 … から誰でも無料でダウンロードできます。非常に面白いです。https://twitter.com/genkuroki/status/694868801892933633 …

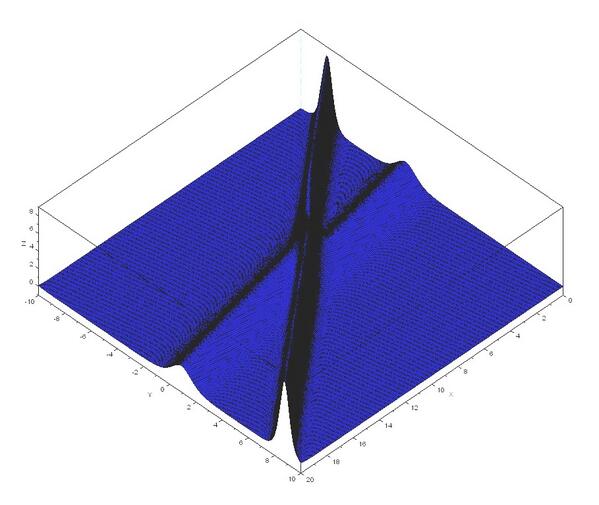
#数楽 https://twitter.com/genkuroki/status/695057739421057024 …コンパクトRiemann面の無限遠点に住んでいて「世界」を支配しているX氏の話はそのままソリトン方程式の佐藤理論によるKP方程式系の準周期解の話になっています。

#数楽 LU分解では計算途中でzero division errorが出ないようにするために「行の置換」が必要になるのですが、ソリトン方程式の佐藤理論の文脈では(転置したスタイルに移っているので)「列の置換」が出て来ます。数学者はWeyl群作用と呼んでいます。続く

#数楽 続き。あ、流儀をまた変えます。最近やっていないので流儀を混乱していました。ソリトン方程式の文脈でよく使われているスタイルはX=W^{-1}Z、Wは対角成分が1の下三角行列、Zは対角部分を含む上三角行列です。これはまさにLU分解。L=W^{-1}、U=Zです。

#数楽 続き。dX=AXをX=W^{-1}Zで書き直すと、-W(dW/dt)W^{-1}Z+W^{-1}(dZ/dt)=AW^{-1}Z∴-(dW/dt)W^{-1}+(dZ/dt)Z^{-1}=WAW^{-1}と左辺は-(対角成分が0の下三角)+(上三角)の形になる。続く

#数楽 だからWAW^{-1}の対角成分を含む上三角部分をBと書くと、(dZ/dt)Z^{-1}=B、-(dW/dt)W^{-1}=WAW^{-1}-BすなわちdZ/dt=BZ、dW/dt=BW-WA.これが所謂Sato-Wilson方程式です。Bは時間依存、Aは定数。

#数楽 続き。行列Xに関する線形微分方程式dX=AXを"LU分解"で書き直すと非線形微分方程式が得られるのですが、KdV方程式のような非線形のソリトン方程式はそのような操作で得られる非線形方程式だということです。ソリトン方程式が「線形化」＝「逆散乱法」によって解けることには～続く

#数楽 続き～以上のようなほぼ大学一年生レベルの超絶シンプルな理解がソリトン方程式の佐藤理論によって得られてしまったわけです。私は佐藤幹夫先生の集中講義を2年続けて聴いたのですが、本当に大学一年生でも聞いてわかるような素朴な巨大行列式(∞×∞)の操作をしまくっていました。続く

#数楽 で、行や列の置換について。行や列の置換の操作もLU分解を通して見直せます。置換行列Pによって列を置換する操作X↦XP=W^{-1}ZPはZPのLU分解をZP=G_P(Z)^{-1}(G_P(Z)ZP) (G_P(Z)は対角成分が1の下三角、残りは上三角)と～続く

#数楽 続き～書くと、X↦XPはW↦G_P(Z)W、Z↦G_P(Z)ZPと書き直されます。だからもしもG_P(Z)の形を具体的に計算できれば列の置換の操作をLU分解を通して見ることができます。一般のPだとややこしいのですが、2つの列の互換のケースなら容易に計算できます。

#数楽 続き。あ、正確に言えば、隣り合った2つの列の互換のケースであればG_P(Z)を容易に計算できます。上三角行列Zの隣り合った2つの列を互換すると2×2のブロック分だけ上三角行列でなくなるのですが、左から対角成分が1の下三角行列をかけて上三角行列にできます。大学1年レベル。

#数楽 続き。ここからがガチで私の専門(研究)の話になるのですが、「隣り合った列の互換」のZ↦G_P(Z)ZPの成分の変換の公式であれば、一般の対称化可能一般Cantan行列(GCM)が定める量子展開環のケースに一般化できます。Weyl群のZへの双有理作用が量子化される！続く

#数楽 続き。量子展開環まで行かなくても、Kac-Moody代数のレベルでの量子化も可能です。(注意：この意味の量子化は正準量子化の意味での量子化、量子展開環の意味での量子化はここではq差分化と解釈される。) LU分解での対角成分＝τ函数の量子化もできています。続く

#数楽 続き。量子化されたτ函数の部分は、色々ミステリアスな感じで、Kac-Moody代数や量子展開環に関する一般論の中のどこに位置付けられるのかを私は理解していません。現時点ではτ函数に関する非可換性を手で入れている感じ。続く

#数楽 続き。量子化する前のτ函数は行列式だという理由でWeyl群作用の結果も(従属変数について)多項式になるのですが、量子化した後は同じ方針で(非可換)多項式性を証明できてなくて、Kac-Moody代数の表現のBGG圏の構造を使って証明するということになっています。続く

#数楽 続き。具体的な計算では非可換分数の計算を必死になってやって最後に分母のある項達が奇跡的にキャンセルして非可換多項式になるということを確認するのですが、証明ではBGG圏の構造を使っている。何か意味ありげでもあり、この証明の方針が最終的なものであるかどうかもわからない。

#数楽 続き。というわけで、私のガチな専門(の一つ)は「LU分解の正準量子化に関係した事柄」と言ってもらって構わないということになっています。素朴には大学一年での線型代数やプログラミングの演習レベルの話なのですが、適切に非可換性を入れて正準量子化すると違う世界が見えて来る。

#数楽 知人のコンサル女子から「LU分解の正準量子化ってなに？」という質問が飛んできたりしないものかなwww